The Data Science Lab
How to Create a Machine Learning Decision Tree Classifier Using C#
After earlier explaining how to compute disorder and split data in his exploration of machine learning decision tree classifiers, resident data scientist Dr. James McCaffrey of Microsoft Research now shows how to use the splitting and disorder code to create a working decision tree classifier.
A decision tree classifier is a machine learning (ML) prediction system that generates rules such as "IF income < 28.0 AND education >= 14.0 THEN politicalParty = 2." Using a decision tree classifier from an ML library is often awkward because in most situations the classifier must be customized and library decision trees have many complex supporting functions. When I need a decision tree classifier, I always create one from scratch.
Implementing a decision tree classifier from scratch involves two main tasks. First, you must write functions related to repeatedly splitting your training data into smaller and smaller subsets based on the amount of disorder in the subsets. Second, you must write code that uses the splitting functions to create a tree data structure that computes a predicted class for a given input. In my previous Data Science Lab column, I explained how to compute disorder and split data. In this column I explain how to use the splitting and disorder code to create a working decision tree classifier.
A good way to see where this article is headed is to take a look at the screenshot of a demo program in Figure 1. The demo begins by setting up 30 data items that are a subset of the 150-item Fisher's Iris dataset. The goal is to predict the species (labelled 0, 1 or 2) of an iris flower based on sepal length and width, and petal length and width.
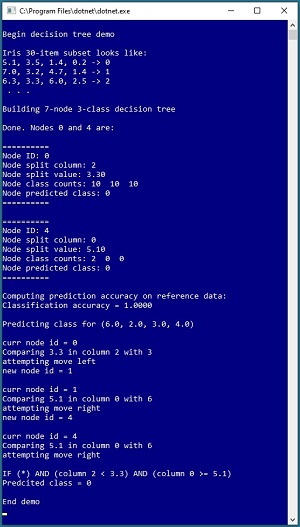[Click on image for larger view.] Figure 1: A Decision Tree Classifier in Action
The demo program uses the 30 items to build a decision tree classifier that has seven nodes. Not too surprisingly, because there are only 30 training/reference data items, the decision tree achieves 100% accuracy when predicting the class of the 30 training items. The demo concludes by predicting the class/species of a new, previously unseen iris flower with sepal and petal values of (6.0, 2.0, 3.0, 4.0). The system walks down the decision tree and predicts that the class is 0, corresponding to the rule "IF (column 2 < 3.1) AND (column 0 >= 5.1) THEN class = 0."
This article assumes you have intermediate or better skill with C# and an understanding of how to use Gini impurity disorder to split a dataset into two subsets which have small average impurity. The code for the demo program shown in Figure 1 is a bit too long to present in its entirety in this article but the complete code is available in the accompanying file download.
Understanding the Data
The demo program uses 30 data items to create a decision tree classifier. The data looks like:
5.1, 3.5, 1.4, 0.2 -> 0
4.9, 3.0, 1.4, 0.2 -> 0
. . .
7.0, 3.2, 4.7, 1.4 -> 1
. . .
7.2, 3.6, 6.1, 2.5 -> 2
Each item has four predictor values: sepal length, sepal width, petal length, petal width. A sepal is a leaf-like structure. Each flower is one of three species: setosa (encoded as 0), versicolor (encoded as 1) and virginica (encoded as 2).
The first 10 data items are setosa, the next 10 are versicolor and the last 10 are virginica. When working with decision tree classifiers it's convenient to encode class labels as 0, 1, 2, and so on, as opposed to one-hot encoding that's often used for neural network classifiers.
Understanding the Decision Tree Structure
When creating a decision tree classifier, there is no standard format so you have many options for designing the tree data structure. The structure used in the demo program is illustrated in Figure 2. Each node in the demo decision tree classifier has six values defined in a Node class:
public class Node
{
public int nodeID;
public List<int> rows;
public int splitCol;
public double splitVal;
public int[] classCounts;
public int predictedClass;
}
The List<int> collection named rows holds the rows associated with a node. The splitCol and splitVal members store the column and value that determine where the source rows in the node should be split to give two subsets with a relatively small average Gini impurity. Small impurity means more homogeneity, which is better. The classCounts array holds the number of each of the classes associated with the source rows in the node. The predictedClass value is the prediction associated with the current node.
For the root node, the nodeID value is 0. The source rows are the rows of the entire 30-item dataset: (0, 1, 2, . . . 29). The splitCol is [2] and the splitVal is 3.3 which means that rows where the value in column [2] is strictly less than 3.3 are assigned to the left child of the root node, and rows where the value in column [2] are greater than or equal to 3.3 are assigned to the right child of the root node.
The classCounts for the root node are the numbers of each class associated with the source rows. Because all 30 rows are in the root node, and there are 10 of each of the three classes, the classCounts array holds [10, 10, 10]. The predictedClass for the root node is the class that corresponds to the highest classCounts value. Because all three class count values are the same, the predicted class is a tie among classes 0, 1 and 2. When ties occur, the demo classifier arbitrarily selects the first of the tied classes so the predicted class in this case is 0.
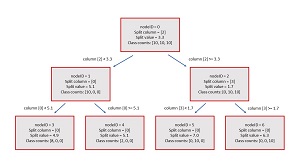[Click on image for larger view.] Figure 2: Structure of the Demo Decision Tree
An important design decision is whether to implement your decision tree classifier using a recursive tree data structure or a list-based data structure. Almost all of the decision tree classifier library implementations I've seen use the recursion approach. But in my opinion, recursive tree classifiers are much, much more difficult to work with than list-based classifiers.
The demo program uses a List<Node> data structure to store nodes is a level-by-level order. Using this organization it's easy to determine the location of any child node or a parent node. If a node index is n, then the node itself is located at index [n] in the list.
The left child of n is located at index [2n + 1], and the right child is located at index [2n + 2]. If n is an odd number, the node is a left child and if n is even the node is a right child. If a node is a left child, its parent is located at index [(n - 1) / 2] and if the node is a right child its parent is at index [(n – 2) / 2]. Simple, easy, and efficient.
The Demo Program
To create the demo program, I launched Visual Studio 2019. I used the Community (free) edition but any relatively recent version of Visual Studio will work fine. From the main Visual Studio start window I selected the "Create a new project" option. Next, I selected C# from the Language dropdown control and Console from the Project Type dropdown, and then picked the "Console App (.NET Core)" item.
The code presented in this article will run as a .NET Core console application or as a .NET Framework application. Many of the newer Microsoft technologies, such as the ML.NET code library, specifically target .NET Core so it makes sense to develop most C# ML code in that environment.
I entered "DecisionTree" as the Project Name, specified C:\VSM on my local machine as the Location (you can use any convenient directory), and checked the "Place solution and project in the same directory" box.
After the template code loaded into Visual Studio, at the top of the editor window I removed all using statements to unneeded namespaces, leaving just the reference to the top-level System namespace. Then I added a reference to the Collections.Generic namespace because the demo code uses the List<int> collection type. The demo needs no other assemblies and uses no external code libraries.
In the Solution Explorer window, I renamed file Program.cs to the more descriptive DecisionTreeProgram.cs and then in the editor window I renamed class Program to class DecisionTreeProgram to match the file name. The structure of the demo program, with a few minor edits to save space, is shown in Listing 1.
Listing 1. Decision Tree Demo Program Structure
using System;
using System.Collections.Generic;
namespace DecisionTree
{
class DecisionTreeProgram
{
static void Main(string[] args)
{
Console.WriteLine("Decision tree demo ");
double[][] dataX = new double[30][];
dataX[0] = new double[] { 5.1, 3.5, 1.4, 0.2 };
dataX[1] = new double[] { 4.9, 3.0, 1.4, 0.2 };
dataX[2] = new double[] { 4.7, 3.2, 1.3, 0.2 };
dataX[3] = new double[] { 4.6, 3.1, 1.5, 0.2 };
dataX[4] = new double[] { 5.0, 3.6, 1.4, 0.2 };
dataX[5] = new double[] { 5.4, 3.9, 1.7, 0.4 };
dataX[6] = new double[] { 4.6, 3.4, 1.4, 0.3 };
dataX[7] = new double[] { 5.0, 3.4, 1.5, 0.2 };
dataX[8] = new double[] { 4.4, 2.9, 1.4, 0.2 };
dataX[9] = new double[] { 4.9, 3.1, 1.5, 0.1 };
dataX[10] = new double[] { 7.0, 3.2, 4.7, 1.4 };
dataX[11] = new double[] { 6.4, 3.2, 4.5, 1.5 };
dataX[12] = new double[] { 6.9, 3.1, 4.9, 1.5 };
dataX[13] = new double[] { 5.5, 2.3, 4.0, 1.3 };
dataX[14] = new double[] { 6.5, 2.8, 4.6, 1.5 };
dataX[15] = new double[] { 5.7, 2.8, 4.5, 1.3 };
dataX[16] = new double[] { 6.3, 3.3, 4.7, 1.6 };
dataX[17] = new double[] { 4.9, 2.4, 3.3, 1.0 };
dataX[18] = new double[] { 6.6, 2.9, 4.6, 1.3 };
dataX[19] = new double[] { 5.2, 2.7, 3.9, 1.4 };
dataX[20] = new double[] { 6.3, 3.3, 6.0, 2.5 };
dataX[21] = new double[] { 5.8, 2.7, 5.1, 1.9 };
dataX[22] = new double[] { 7.1, 3.0, 5.9, 2.1 };
dataX[23] = new double[] { 6.3, 2.9, 5.6, 1.8 };
dataX[24] = new double[] { 6.5, 3.0, 5.8, 2.2 };
dataX[25] = new double[] { 7.6, 3.0, 6.6, 2.1 };
dataX[26] = new double[] { 4.9, 2.5, 4.5, 1.7 };
dataX[27] = new double[] { 7.3, 2.9, 6.3, 1.8 };
dataX[28] = new double[] { 6.7, 2.5, 5.8, 1.8 };
dataX[29] = new double[] { 7.2, 3.6, 6.1, 2.5 };
int[] dataY =
new int[30] { 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
2, 2, 2, 2, 2, 2, 2, 2, 2, 2 };
Console.WriteLine("Iris 30-item subset: ");
Console.WriteLine("5.1, 3.5, 1.4, 0.2 -> 0");
Console.WriteLine("7.0, 3.2, 4.7, 1.4 -> 1");
Console.WriteLine("6.3, 3.3, 6.0, 2.5 -> 2");
Console.WriteLine(" . . . ");
Console.WriteLine("Build 7-node 3-class tree");
DecisionTree dt = new DecisionTree(7, 3);
dt.BuildTree(dataX, dataY);
// Console.WriteLine("Tree is: ");
// dt.Show(); // show all nodes in tree
Console.WriteLine("Done. Nodes 0 and 4 are:");
dt.ShowNode(0);
dt.ShowNode(4);
Console.WriteLine("Computing accuracy:");
double acc = dt.Accuracy(dataX, dataY);
Console.WriteLine("Classification accuracy = " +
acc.ToString("F4"));
double[] x = new double[] {6.0, 2.0, 3.0, 4.0};
Console.Write("Predicting class for");
Console.WriteLine(" (6.0, 2.0, 3.0, 4.0)");
int predClass = dt.Predict(x, verbose: true);
Console.WriteLine("End demo ");
Console.ReadLine();
} // Main
} // Program class
class DecisionTree
{
public int numNodes;
public int numClasses;
public List<Node> tree;
public DecisionTree(int numNodes,
int numClasses) { . . }
public void BuildTree(double[][] dataX,
int[] dataY) { . . }
public void Show() { . . }
public void ShowNode(int nodeID) { . . }
public int Predict(double[] x,
bool verbose) { . . }
public double Accuracy(double[][] dataX,
int[] dataY) { . . }
private static SplitInfo GetSplitInfo(
double[][] dataX, int[] dataY, List<int> rows,
int numClasses) { . . }
private static double Impurity(int[] dataY,
List<int> rows, int numClasses) { . . }
private static double MeanImpurity(int[] dataY,
List<int> rows1, List<int> rows2,
int numClasses) { . . }
private static int[] ComputeClassCts(int[] dataY,
List<int> rows, int numClasses) { . . }
private static int ArgMax(int[] classCts) { . . }
// ----------
public class Node
{
public int nodeID;
public List<int> rows;
public int splitCol;
public double splitVal;
public int[] classCounts;
public int predictedClass;
}
public class SplitInfo // helper
{
public int splitCol;
public double splitVal;
public List<int> lessRows;
public List<int> greaterRows;
}
// ----------
} // DecisionTree class
} // ns
Although implementing a decision tree classifier is by no means trivial, the code is not as difficult to understand as it might first appear. All of the program logic is contained in the Main method. The decision tree classifier is encapsulated in a class named DecisionTree. The program uses a container class named SplitInfo to hold values related to splitting a node into a left child and a right child based on Gini impurity.
Class DecisionTree has six public methods. The constructor accepts the number of nodes to create and the number of classes in the data. Method BuildTree() uses the training/reference data to create a tree such as the one shown in Figure 2. Methods ShowNode() and Show() can be used to inspect a single node or all nodes in a decision tree.
Public method Predict() accepts an input vector of predictor values and computes a predicted class. Predict() has a parameter named verbose that controls how much information is shown as the method walks through the decision tree. Method Accuracy() accepts a matrix of predictor values and a vector of known correct class labels, and returns the percentage of correct predictions.