The Data Science Lab
Gaussian Process Regression Using the scikit Library
Many data scientists avoid tricky GPR because of its complex mathematics, but when it works, it often works very well.
A regression problem is one where the goal is to predict a single numeric value. For example, you might want to predict the price of a house based on its square footage, age, number of bedrooms and property tax rate. Note that the common "logistic regression" machine learning technique is a binary classification system (predict one of two possible discrete values) in spite of its name.
There are many different techniques available to create a regression model. Some common techniques, listed from less complex to more complex, are: linear regression, linear lasso regression, linear ridge regression, k-nearest neighbors regression, (plain) kernel regression, kernel ridge regression, Gaussian process regression, decision tree regression and neural network regression. This article explains how to create and use Gaussian process regression (GPR) models. Compared to other regression techniques, GPR is especially useful when there is limited training data.
There are several tools and code libraries that you can use to create a GPR model. The scikit-learn library (also called scikit or sklearn) is based on the Python language and is one of the most popular.
A good way to see where this article is headed is to take a look at the screenshot in Figure 1. The demo program loads a 200-item set of training data and a 40-item set of test data into memory. The data is synthetic. Next, the demo creates and trains a GPR model using the scikit GaussianProcessRegressor module.
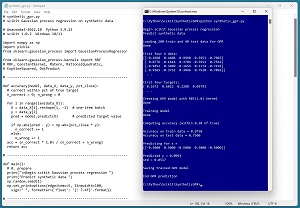[Click on image for larger view.] Figure 1: Gaussian Process Regression in Action /figcaption>
After training, the model is applied to the training data and the test data. The model scores 97.50 percent accuracy (195 correct out of 200) on the training data, and 75.00 percent accuracy (30 correct out of 40) on the test data. The demo program defines a correct prediction as one that's within 10 percent of the true target value.
The demo concludes by predicting the target value of a new, previously unseen data item with predictor x values of (-0.5, 0.5, -0.5, 0.5, -0.5). The predicted y value is 0.0993 with a standard deviation of 0.0517.
This article assumes you have intermediate or better skill with a C-family programming language, but doesn't assume you know much about Gaussian process regression or the scikit library. The complete source code for the demo program is presented in this article and in the accompanying file download. The source code and data are also available online.
Installing the scikit Library
There are several ways to install the scikit library. I recommend installing the Anaconda Python distribution. Anaconda contains a core Python engine plus over 500 libraries that are (mostly) compatible with each other. I used Anaconda3-2022.10, which contains Python 3.9.13 and the scikit 1.0.2 version. The demo code runs on Windows 10 or 11.
Briefly, Anaconda / Python / scikit is installed using a Windows self-extracting executable file. The setup process is mostly straightforward and takes about 15 minutes following step-by-step instructions.
There are more up-to-date versions of Anaconda / Python / scikit library available. But because the Python ecosystem has hundreds of libraries, if you install the most recent versions of these libraries, you run a greater risk of library incompatibilities -- this is a major headache when working with Python.
The Data
The data is synthetic and was generated by a 5-10-1 neural network with random weights and biases. The point is that there is an underlying model that should be discoverable to some extent (as opposed to purely random data).
There are 200 training items and 40 test items. The structure of data looks like:
-0.1660 0.4406 -0.9998 -0.3953 -0.7065 0.1672
0.0776 -0.1616 0.3704 -0.5911 0.7562 0.6022
-0.9452 0.3409 -0.1654 0.1174 -0.7192 0.2288
0.9365 -0.3732 0.3846 0.7528 0.7892 0.0379
. . .
Each line of tab-delimited data has five predictor values followed by the target value to predict. The predictor values are all between -1.0 and +1.0 (corresponding to real data that has been normalized). The target values are all between 0.0 and 1.0.
Gaussian process regression was designed for problems with strictly numeric predictor variables. However, GPR can be used with categorical predictor variables by using one-hot encoding. For example, if the source data has a variable Color with possible values red, blue, green and yellow, then red can be encoded as 1000, blue = 0100, green = 0010 and yellow = 0001.
When using GPR you should normalize numeric predictor variables so that all values are roughly in the same range. This prevents variables with large magnitudes, such as annual income, from overwhelming variables with small values, such as college GPA.
Understanding Gaussian Process Regression
The mathematics of Gaussian process regression is complex. There are hundreds of web pages and hundreds of hours of video that attempt to explain GPR. The mere fact that there are so many resources available is an indication of how tricky the topic is.
There is no single best resource for GPR theory -- it all depends on a person's background and extent of understanding of topics including kernel functions, covariance matrices, multivariate Gaussian distributions, regularization, Bayesian mathematics and matrix operations. That said, it is possible to create effective GPR prediction models using the scikit library without having deep knowledge of the underlying theory.
A key concept of GPR is the idea of a kernel function. A kernel function accepts two vectors and computes a measure of similarity/dissimilarity. There are many different types of kernel functions and each type has several variations.
One of the most commonly used kernel functions is the radial basis function (RBF). The variation of RBF used by the scikit GaussianProcessRegressor module is rbf(x1, x2) = exp( -1 * ||x1 - x2||^2 / (2 * s^2) ) where x1 and x2 are vectors. The ||x1 - x2||^2 term is squared Euclidean distance between x1 and x2. The s term is the length scale and is a constant that must be specified.
Suppose x1 = (0.4, 0.8, 0.2) and x2 = (0.1, 0.6, 0.3) and s = 1.0. Then:
||x1 - x2||^2 = (0.4 - 0.1)^2 + (0.8 - 0.6)^2 + (0.2 - 0.3)^2
= 0.09 + 0.04 + 0.01
= 0.14
and therefore:
rbf(x1, x2) = exp( -1 * ||x1 - x2||^2 / (2 * s^2) )
= exp( -1 * 0.14 / (2 * 1.0^2) )
= exp(-0.07)
= 0.9324
In addition to the RBF kernel function, the scikit GaussianProcessRegressor module supports the ConstantKernel, Matern, RationalQuadratic, ExpSineSquared and DotProduct kernel functions. The main challenge when using GPR is finding a good kernel function. There are few rules of thumb, and it's mostly a matter of trial and error guided by experience.
The Demo Program
The complete demo program is presented in Listing 1. Notepad is my code editor of choice but most of my colleagues prefer one of the many excellent IDEs that are available for Python. I indent my Python program using two spaces rather than the more common four spaces.
The program imports the NumPy library, which contains numeric array functionality, the pickle module used for saving a trained model, and the GaussianProcessRegressor module, which contains GPR functionality. Notice the name of the root scikit module is sklearn rather than scikit.
import numpy as np
import pickle
from sklearn.gaussian_process import GaussianProcessRegressor
In terms of Python style, I prefer to place all the import statements at the top of a program. An alternative is to place each import statement near its first usage.
Listing 1: Complete Demo Program
# synthetic_gpr.py
# scikit Gaussian process regression on synthetic data
# Anaconda3-2022.10 Python 3.9.13
# scikit 1.0.2 Windows 10/11
import numpy as np
import pickle
from sklearn.gaussian_process import GaussianProcessRegressor
from sklearn.gaussian_process.kernels import RBF
# RBF, ConstantKernel, Matern, RationalQuadratic,
# ExpSineSquared, DotProduct
# -----------------------------------------------------------
def accuracy(model, data_X, data_y, pct_close):
# correct within pct of true target
n_correct = 0; n_wrong = 0
for i in range(len(data_X)):
X = data_X[i].reshape(1, -1) # one-item batch
y = data_y[i]
pred = model.predict(X) # predicted target value
if np.abs(pred - y) < np.abs(pct_close * y):
n_correct += 1
else:
n_wrong += 1
acc = (n_correct * 1.0) / (n_correct + n_wrong)
return acc
# -----------------------------------------------------------
def main():
# 0. prepare
print("\nBegin scikit Gaussian process regression ")
print("Predict synthetic data ")
np.random.seed(1)
np.set_printoptions(edgeitems=5, linewidth=100,
sign=" ", formatter={'float': '{: 7.4f}'.format})
# -----------------------------------------------------------
# 1. load data
print("\nLoading 200 train and 40 test data for GPR ")
train_file = ".\\Data\\synthetic_train.txt"
train_X = np.loadtxt(train_file, delimiter="\t",
usecols=(0,1,2,3,4),
comments="#", dtype=np.float64)
train_y = np.loadtxt(train_file, delimiter="\t",
usecols=5, comments="#", dtype=np.float64)
test_file = ".\\Data\\synthetic_test.txt"
test_X = np.loadtxt(test_file, delimiter="\t",
usecols=(0,1,2,3,4),
comments="#", dtype=np.float64)
test_y = np.loadtxt(test_file, delimiter="\t",
usecols=5, comments="#", dtype=np.float64)
print("Done ")
print("\nFirst four X data: ")
print(train_X[0:4][:])
print(". . .")
print("\nFirst four targets: ")
print(train_y[0:4])
print(". . .")
# -----------------------------------------------------------
# 2. create and train GPR model
print("\nCreating GPR model with RBF(1.0) kernel ")
# GaussianProcessRegressor(kernel=None, *, alpha=1e-10,
# optimizer='fmin_l_bfgs_b', n_restarts_optimizer=0,
# normalize_y=False, copy_X_train=True, random_state=None)
#
# default: ConstantKernel(1.0, constant_value_bounds="fixed")
# * RBF(1.0, length_scale_bounds="fixed")
# scikit-learn.org/stable/modules/gaussian_process.html
krnl = RBF(length_scale=1.0, length_scale_bounds="fixed")
gpr_model = GaussianProcessRegressor(kernel=krnl,
normalize_y=False, random_state=1, alpha=0.001)
print("Done ")
print("\nTraining model ")
gpr_model.fit(train_X, train_y)
print("Done ")
# -----------------------------------------------------------
# 3. compute model accuracy
print("\nComputing accuracy (within 0.10 of true) ")
acc_train = accuracy(gpr_model, train_X, train_y, 0.10)
print("\nAccuracy on train data = %0.4f " % acc_train)
acc_test = accuracy(gpr_model, test_X, test_y, 0.10)
print("Accuracy on test data = %0.4f " % acc_test)
# 4. use model to predict
x = np.array([[-0.5, 0.5, -0.5, 0.5, -0.5]],
dtype=np.float64)
print("\nPredicting for x = ")
print(x)
(y_pred, std) = gpr_model.predict(x, return_std=True)
print("\nPredicted y = %0.4f " % y_pred)
print("std = %0.4f " % std)
# 5. save model
print("\nSaving trained GPR model ")
fn = ".\\Models\\gpr_model.pkl"
with open(fn,'wb') as f:
pickle.dump(gpr_model, f)
print("\nEnd GPR prediction ")
# -----------------------------------------------------------
if __name__ == "__main__":
main()
All the program logic is contained in a main() function. The demo defines an accuracy() function that emphasizes clarity at the expense of efficiency. The demo begins by setting the NumPy random seed:
def main():
# 0. prepare
print("Begin scikit Gaussian process regression ")
print("Predict synthetic data ")
np.random.seed(1)
np.set_printoptions(edgeitems=5, linewidth=100,
sign=" ", formatter={'float': '{: 7.4f}'.format})
. . .
Technically, setting the random seed value isn't necessary, but doing so helps you to get reproducible results in many situations where there are one or more random components. The GaussianProcessRegressor module can be instructed to try to programmatically optimize its kernel function parameters, and that code has a random component.
Loading the Training and Test Data
The demo program loads the training data into memory using these statements:
# 1. load data
print("Loading 200 train and 40 test data for GPR ")
train_file = ".\\Data\\synthetic_train.txt"
train_X = np.loadtxt(train_file, delimiter="\t",
usecols=(0,1,2,3,4),
comments="#", dtype=np.float64) # 2-D
train_y = np.loadtxt(train_file, delimiter="\t",
usecols=5, comments="#", dtype=np.float64) # 1-D
This code assumes the data files are stored in a directory named Data. There are many ways to load data into memory. I prefer using the NumPy library loadtxt() function, but a common alternative is the Pandas library read_csv() function.
The code reads training and test data using one call to loadtxt() for the predictor values and a second call to loadtxt() for the target values. An alternative approach is to read both predictor and target values into a matrix using a single call to loadtxt() and then split the matrix into a matrix of predictors and a vector of target values.
The 40-item test data is read into memory in the same way as the training data:
test_file = ".\\Data\\synthetic_test.txt"
test_X = np.loadtxt(test_file, delimiter="\t",
usecols=(0,1,2,3,4),
comments="#", dtype=np.float64)
test_y = np.loadtxt(test_file, delimiter="\t",
usecols=5, comments="#", dtype=np.float64)
print("Done ")