The Data Science Lab
Neural Regression Using PyTorch: Defining a Network
Dr. James McCaffrey of Microsoft Research presents the second of four machine learning articles that detail a complete end-to-end production-quality example of neural regression using PyTorch.
The goal of a regression problem is to predict a single numeric value, for example, predicting the price of a used car based on variables such as mileage, brand and year manufactured. There are several classical statistics techniques for regression problems. Neural regression solves a regression problem using a neural network. This article is the second in a series of four articles that present a complete end-to-end production-quality example of neural regression using PyTorch. The recurring example problem is to predict the price of a house based on its area in square feet, air conditioning (yes or no), style ("art_deco," "bungalow," "colonial") and local school ("johnson," "kennedy," "lincoln").
The process of creating a PyTorch neural network for regression consists of six steps:
- Prepare the training and test data
- Implement a Dataset object to serve up the data in batches
- Design and implement a neural network
- Write code to train the network
- Write code to evaluate the model (the trained network)
- Write code to save and use the model to make predictions for new, previously unseen data
Each of the six steps is complicated. And the six steps are tightly coupled which adds to the difficulty. This article covers the third step -- designing and implementing a neural network for neural regression.
A good way to see where this series of articles is headed is to take a look at the screenshot of the demo program in
Figure 1
. The demo begins by creating Dataset and DataLoader objects which have been designed to work with the house data. Next, the demo creates an 8-(10-10)-1 deep neural network. The demo prepares training by setting up a loss function (mean squared error), a training optimizer function (Adam) and parameters for training (learning rate and max epochs).
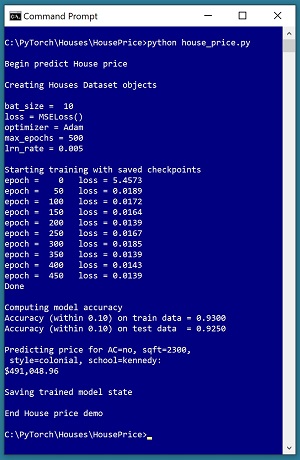[Click on image for larger view.] Figure 1: Neural Regression in Action
The demo trains the neural network for 500 epochs in batches of 10 items. An epoch is one complete pass through the training data. The training data has 200 items, therefore, one training epoch consists of processing 20 batches of 10 training items.
During training, the demo computes and displays a measure of the current error (also called loss) every 50 epochs. Because error slowly decreases, it appears that training is succeeding. Behind the scenes, the demo program saves checkpoint information after every 50 epochs so that if the training machine crashes, training can be resumed without having to start from the beginning.
After training the network, the demo program computes the prediction accuracy of the model based on whether or not the predicted house price is within 10 percent of the true house price. The accuracy on the training data is 93.00 percent (186 out of 200 correct) and the accuracy on the test data is 92.50 percent (37 out of 40 correct). Because the two accuracy values are similar, it is likely that model overfitting has not occurred.
Next, the demo uses the trained model to make a prediction on a new, previously unseen house. The raw input is (air conditioning = "no", square feet area = 2300, style = "colonial", school = "kennedy"). The raw input is normalized and encoded as (air conditioning = -1, area = 0.2300, style = 0,0,1, school = 0,1,0). The computed output price is 0.49104896 which is equivalent to $491,048.96 because the raw house prices were all normalized by dividing by 1,000,000.
The demo program concludes by saving the trained model using the state dictionary approach. This is the most common of three standard techniques.
This article assumes you have an intermediate or better familiarity with a C-family programming language, preferably Python, but doesn't assume you know very much about PyTorch. The complete source code for the demo program, and the two data files used, are available in the download that accompanies this article. All normal error checking code has been omitted to keep the main ideas as clear as possible.
To run the demo program, you must have Python and PyTorch installed on your machine. The demo programs were developed on Windows 10 using the Anaconda 2020.02 64-bit distribution (which contains Python 3.7.6) and PyTorch version 1.7.0 for CPU installed via pip. You can find detailed step-by-step installation instructions for this configuration in my
blog post
.
The House Data
The raw House data is synthetic and was generated programmatically. There are a total of 240 data items, divided into a 200-item training dataset and a 40-item test dataset. The raw data looks like:
no 1275 bungalow $318,000.00 lincoln
yes 1100 art_deco $335,000.00 johnson
no 1375 colonial $286,000.00 kennedy
yes 1975 bungalow $512,000.00 lincoln
. . .
no 2725 art_deco $626,000.00 kennedy
Each line of tab-delimited data represents one house. The value to predict, house price, is in 0-based column [3]. The predictors variables in columns [0], [1], [2] and [4] are air conditioning, area in square feet, style and local school. For simplicity, there are just three house styles and three schools.
House area values were normalized by dividing by 10,000 and house prices were normalized by dividing by 1,000,000. Air conditioning was binary encoded as no = -1, yes = +1. Style was one-hot encoded as "art_deco" = (1,0,0), "bungalow" = (0,1,0), "colonial" = (0,0,1). School was one-hot encoded as "johnson" = (1,0,0), "kennedy" = (0,1,0), "lincoln" = (0,0,1). The resulting normalized and encoded data looks like:
-1 0.1275 0 1 0 0.3180 0 0 1
1 0.1100 1 0 0 0.3350 1 0 0
-1 0.1375 0 0 1 0.2860 0 1 0
1 0.1975 0 1 0 0.5120 0 0 1
. . .
-1 0.2725 1 0 0 0.6260 0 1 0
After the structure of the training and test files was established, I designed and coded a PyTorch Dataset class to read the house data into memory and serve the data up in batches using a PyTorch DataLoader object. A Dataset class definition for the normalized encoded House data is shown in Listing 1.
Listing 1: A Dataset Class for the Student Data
class HouseDataset(T.utils.data.Dataset):
# AC sq ft style price school
# -1 0.2500 0 1 0 0.5650 0 1 0
# 1 0.1275 1 0 0 0.3710 0 0 1
# air condition: -1 = no, +1 = yes
# style: art_deco, bungalow, colonial
# school: johnson, kennedy, lincoln
def __init__(self, src_file, m_rows=None):
all_xy = np.loadtxt(src_file, max_rows=m_rows,
usecols=[0,1,2,3,4,5,6,7,8], delimiter="\t",
comments="#", skiprows=0, dtype=np.float32)
tmp_x = all_xy[:,[0,1,2,3,4,6,7,8]]
tmp_y = all_xy[:,5].reshape(-1,1) # 2-D
self.x_data = T.tensor(tmp_x, \
dtype=T.float32).to(device)
self.y_data = T.tensor(tmp_y, \
dtype=T.float32).to(device)
def __len__(self):
return len(self.x_data)
def __getitem__(self, idx):
preds = self.x_data[idx,:] # or just [idx]
price = self.y_data[idx,:]
return (preds, price) # tuple of matrices
Preparing data and defining a PyTorch Dataset is not trivial. You can find the article that explains how to create Dataset objects and use them with DataLoader objects
here
.
The Overall Program Structure
The overall structure of the PyTorch neural regression program, with a few minor edits to save space, is shown in
Listing 2
. I prefer to indent my Python programs using two spaces rather than the more common four spaces.
Listing 2: The Structure of the Demo Program
# house_price.py
# PyTorch 1.7.0-CPU Anaconda3-2020.02
# Python 3.7.6 Windows 10
import numpy as np
import time
import torch as T
device = T.device("cpu")
class HouseDataset(T.utils.data.Dataset):
# AC sq ft style price school
# -1 0.2500 0 1 0 0.5650 0 1 0
# 1 0.1275 1 0 0 0.3710 0 0 1
# air condition: -1 = no, +1 = yes
# style: art_deco, bungalow, colonial
# school: johnson, kennedy, lincoln
def __init__(self, src_file, m_rows=None): . . .
def __len__(self): . . .
def __getitem__(self, idx): . . .
# ----------------------------------------------------
def accuracy(model, ds): . . .
# ----------------------------------------------------
class Net(T.nn.Module):
def __init__(self): . . .
def forward(self, x): . . .
# ----------------------------------------------------
def main():
# 0. get started
print("Begin predict House price ")
T.manual_seed(4)
np.random.seed(4)
# 1. create Dataset and DataLoader objects
# 2. create neural network
# 3. train network
# 4. evaluate model
# 5. make a prediction
# 6. save model
print("End House price demo ")
if __name__== "__main__":
main()
It's important to document the versions of Python and PyTorch being used because both systems are under continuous development. Dealing with versioning incompatibilities is a significant headache when working with PyTorch and is something you should not underestimate. The demo program imports the Python time module to timestamp saved checkpoints.
I prefer to use "T" as the top-level alias for the torch package. Most of my colleagues don't use a top-level alias and spell out "torch" many times per program. Also, I use the full form of submodules rather than supplying aliases such as "import torch.nn.functional as functional." In my opinion, using the full form is easier to understand and less error-prone than using many aliases.
The demo program defines a program-scope CPU device object. I usually develop my PyTorch programs on a desktop CPU machine. After I get that version working, converting to a CUDA GPU system only requires changing the global device object to T.device("cuda") plus a minor amount of debugging.
The demo program sets the NumPy and PyTorch random number generator seed values so that program runs will be reproducible. The seed value of 4 was used only because it gives representative results.
The demo program defines just one helper method, accuracy(). All of the rest of the program control logic is contained in a main() function. It is possible to define other helper functions such as train_net(), evaluate_model(), and save_model(), but in my opinion this modularization approach makes the program more difficult to understand rather than easier to understand.
Defining a Neural Network for Neural Regression
The first step when designing a PyTorch neural network class for a regression problem is to determine its architecture. Neural architecture design includes the number of input and output nodes, the number of hidden layers and the number of nodes in each hidden layer, the activation functions for the hidden and output layers, and the initialization algorithms for the hidden and output layer nodes.
The number of input nodes is determined by the number of predictor values (after normalization and encoding), eight in the case of the House data. For most regression problems, there is just one output node, which holds the numeric value to predict. It is possible for a neural regression system to have two or more numeric values, but these problems are quite rare.
The demo network uses two hidden layers, each with 10 nodes, resulting in an 8-(10-10)-1 network. The number of hidden layers and the number of nodes in each layer are hyperparameters. Their values must be determined by trial and error guided by experience. The term "AutoML" is sometimes used for any system that programmatically, to some extent, tries to determine good hyperparameter values.
More hidden layers and more hidden nodes are not always better. The Universal Approximation Theorem (sometimes called the Cybenko Theorem) says, loosely, that for any neural architecture with multiple hidden layers, there is an equivalent architecture that has just one hidden layer. For example, a neural network that has two hidden layers with 5 nodes each, is roughly equivalent to a network that has one hidden layer with 25 nodes.
The definition of class Net is shown in Listing 3. In general, most of my colleagues and I use the term "network" or "net" to describe a neural network before it's been trained, and the term "model" to describe a neural network after it's been trained. However, the two terms are often used interchangeably.
Listing 3: Neural Regression Neural Network Definition
class Net(T.nn.Module):
def __init__(self):
super(Net, self).__init__()
self.hid1 = T.nn.Linear(8, 10) # 8-(10-10)-1
self.hid2 = T.nn.Linear(10, 10)
self.oupt = T.nn.Linear(10, 1)
T.nn.init.xavier_uniform_(self.hid1.weight)
T.nn.init.zeros_(self.hid1.bias)
T.nn.init.xavier_uniform_(self.hid2.weight)
T.nn.init.zeros_(self.hid2.bias)
T.nn.init.xavier_uniform_(self.oupt.weight)
T.nn.init.zeros_(self.oupt.bias)
def forward(self, x):
z = T.relu(self.hid1(x))
z = T.relu(self.hid2(z))
z = self.oupt(z) # no activation
return z
The Net class inherits from torch.nn.Module which provides much of the complex behind-the-scenes functionality. The most common structure for a neural regression network is to define the network layers and their associated weights and biases in the __init__() method, and the input-output computations in the forward() method.
The __init__() Method
The __init__() method begins by defining the demo network's three layers of nodes:
def __init__(self):
super(Net, self).__init__()
self.hid1 = T.nn.Linear(8, 10) # 8-(10-10)-1
self.hid2 = T.nn.Linear(10, 10)
self.oupt = T.nn.Linear(10, 1)