The Data Science Lab
How to Train a Machine Learning Radial Basis Function Network Using C#
A radial basis function network (RBF network) is a software system that's similar to a single hidden layer neural network, explains Dr. James McCaffrey of Microsoft Research, who uses a full C# code sample and screenshots to show how to train an RBF network classifier.
A radial basis function network (RBF network) is a software system that is similar to a single hidden layer neural network. In this article I explain how to train an RBF network classifier. I use the C# language but you shouldn't have any trouble refactoring the demo code to another programming language if you wish.
A good way to see where this article is headed is to take a look at the demo program shown in the screenshot in Figure 1 and the graph in Figure 2. The demo begins by setting up a 2-15-3 RBF network. There are two input nodes, 15 hidden nodes, and three output nodes. You can imagine that the RBF network corresponds to a problem where the goal is to predict a person's political leaning (conservative, moderate, liberal) based on their age and annual income.
The number of input and number of output nodes in an RBF network are determined by the problem data, but the number of hidden nodes (15 in the demo) is a hyperparameter that must be determined by trial and error.
There are 28 training items. The data is artificial and was crafted so that simple linear classification techniques, such as multi-class logistic regression and linear SVM, would fail.
The demo program sets values for three training hyperparameters: a learning rate (0.0050), maximum number of iterations (1000), and a single sigma value for the network (0.10). During training, the classification mean squared error slowly decreases from an initial 0.6654 to 0.3272, indicating that training is working.
After training completes, the demo makes a prediction for a new, previously unseen data item with normalized predictor values (0.15, 0.25). The output of the trained RBF model is (0.1354, 0.3190, 0.5455). If the three classes to predict are conservative = (1, 0, 0), moderate = (0, 1, 0), and liberal = (0, 0, 1) then the predicted class would be liberal.
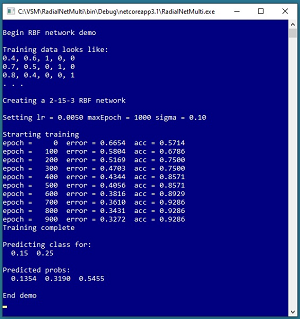[Click on image for larger view.] Figure 1: RBF Network Training Demo
This article assumes you have intermediate or better skill with C# and a solid understanding of RBF network architecture and the RBF network input-output mechanism but doesn’t assume you know anything about training RBF networks. You can find an article explaining RBF network architecture and IO in the list of Visual Studio Magazine Data Science Lab articles.
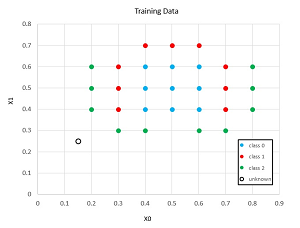[Click on image for larger view.] Figure 2: Training Data
The code for demo program is a bit too long to present in its entirety in this article but the complete source code is available in the associated file download.
Understanding RBF Network Training
The diagram in Figure 3 shows the architecture of a 3-4-2 RBF network. There are three input nodes, or equivalently, an input vector with three values. There are four hidden nodes. Each hidden node has a centroid which is a vector with the same number of values as the input. RBF centroids are usually given the symbol Greek lowercase mu (μ) or English lowercase u.
Each hidden node has a width (sometimes called a standard deviation) which is a single numeric value. RBF widths are usually given the symbol Greek lowercase sigma (σ) or English lowercase s. And each hidden node has a node value which is a single numeric value. There is no standard symbol for a hidden node value.
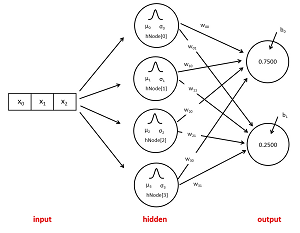[Click on image for larger view.] Figure 3: Example 3-4-2 RBF Network Architecture
The 3-4-2 RBF network in Figure 3 has two output nodes. For an RBF classifier network, the output node values will be normalized so that they sum to 1.0 (for example 0.75 and 0.25) and can be loosely interpreted as probabilities. Each output node has an associated bias value. Bias values are usually given the symbol Greek lowercase beta ( β) or English lowercase b.
An RBF network has a weight value associated with each hidden-to-output node connection. A 3-4-2 network has 4 * 2 = 8 weights. The 2-15-3 RBF demo network has 15 * 3 = 45 weights.
The computed output of an RBF network depends on the input values, and the values of the centroids, the widths, the weights and the biases. Training an RBF network is the process of finding the values of the centroids, widths, weights and biases.
Setting the Values of the Hidden Node Centroids and Widths
There are several approaches for specifying the values of the centroids. The approach I recommend is to select random training items and use them as the values of the centroids. For example, the demo 2-15-3 RBF network requires 15 centroids, where each centroid has two values. The demo training data has 28 items. To supply values for the centroids, the demo Train() method selects 15 of the 28 training items and then copies the values of the 15 selected training items to the 15 RBF centroids.
Suppose you have a 2-4-3 RBF network and you have 8 training data items:
[0] (0.1, 0.19) -> (1, 0, 0)
[1] (0.2, 0.18) -> (0, 1, 0)
[2] (0.3, 0.17) -> (0, 0, 1)
[3] (0.4, 0.16) -> (0, 1, 0)
[4] (0.5, 0.15) -> (1, 0, 0)
[5] (0.6, 0.14) -> (0, 0, 1)
[6] (0.7, 0.13) -> (0, 1, 0)
[7] (0.8, 0.12) -> (1, 0, 0)
To select four random items, first you'd set up an ordered array of eight indices:
(0, 1, 2, 3, 4, 5, 6, 7)
Then you shuffle the indices using the Fisher-Yates mini-algorithm giving something like:
(6, 7, 0, 5, 1, 3, 4, 2)
Then you'd use the first four shuffled indices to pluck off four training items:
[6] (0.7, 0.13)
[7] (0.8, 0.12)
[0] (0.1, 0.19)
[5] (0.6, 0.14)
And then you'd copy these values into the four centroids. Notice that this approach for setting the values of the centroids isn't at all like machine learning training in the usual sense where you iteratively find better values.
There are several approaches for setting the values of the hidden node widths. The approach I recommend is to use a single value for all widths. For example, the demo program sets all 15 widths to 0.10. This value was found by trial and error.
RBF networks are highly sensitive to the value(s) of the hidden node widths and finding good value(s) for the widths is often the biggest challenge when training an RBF network. Researchers have tried many complex algorithms for setting the values of RBF widths but there is no solid evidence that any of these complex technique work better than using a single common width value.
Training the Values of the Weights and Biases
The most common technique for training the values of RBF network weights and biases (which can be thought of as special weights) is to use one of several forms of stochastic gradient descent.
[Click on image for larger view.] Figure 4: The RBF Weight Update Equation
The underlying error function and the weight update equation, in math form, are shown in Figure 4. In words, the error is one half the sum of the squared target values minus output values. For example, suppose there are just three training items:
targets computed output
---------------------------
(0, 1, 0) (0.1, 0.7, 0.3)
(1, 0, 0) (0.6, 0.2, 0.2)
(0, 0, 1) (0.4, 0.1, 0.5)
The error of the first item is (0 – 0.1)^2 + (1 – 0.7)^2 + (0 – 0.3)^2 = 0.01 + 0.09 + 0.09 = 0.19. Similarly, the error of the second item is 0.24 and the error of the third item is 0.42. The total error is 1/2 * (0.19 + 0.24 + 0.42). The one-half term is included only so that the derivative of the error is simpler. In practice, you usually just compute mean squared error, which for the three example items, would be (0.19 + 0.24 + 0.42) / 3. Notice that all three training items are correctly predicted because the largest computed output probability corresponds to the 1 value in the target.
In the weight update equation, delta wjk is the amount to add to the weight connecting hidden node j with output node k. Greek letter eta (η) is the learning rate which moderates the weight delta. The symbol hj is the value of hidden node j. The tk term is the target value for output node k and the ok term is the computed output value for output node k.
The mysterious-looking -1 term in the weight update equation is included so only the weight delta is added to the current weight value, rather than subtracted. This is the common form used in standard neural network training, so I use that convention for RBF networks too.
The Demo Program
To create the demo program, I launched Visual Studio 2019. I used the Community (free) edition but any relatively recent version of Visual Studio will work fine. From the main Visual Studio start window I selected the "Create a new project" option. Next, I selected C# from the Language dropdown control and Console from the Project Type dropdown, and then picked the "Console App (.NET Core)" item.
The code presented in this article will run as a .NET Core console application or as a .NET Framework application. Many of the newer Microsoft technologies, such as the ML.NET code library, specifically target the .NET Core framework so it makes sense to develop most new C# machine learning code in that environment.
I entered "RadialNetMulti" as the Project Name, specified C:\VSM on my local machine as the Location (you can use any convenient directory), and checked the "Place solution and project in the same directory" box.
After the template code loaded into Visual Studio, at the top of the editor window I removed all using statements to unneeded namespaces, leaving just the reference to the top-level System namespace. The demo needs no other assemblies and uses no external code libraries.
In the Solution Explorer window, I renamed file Program.cs to the more descriptive RadialNetMultiProgram.cs and then in the editor window I renamed class Program to class RadialNetMultiProgram to match the file name. The structure of the demo program, with a few minor edits to save space, is shown in Listing 1.
Listing 1. RBF Network Training Demo Program
using System;
namespace RadialNetMulti
{
class RadialNetMultiProgram
{
static void Main(string[] args)
{
Console.WriteLine("Begin RBF network demo ");
double[][] trainX = new double[28][];
trainX[0] = new double[] { 0.4, 0.6 }; // 0
trainX[1] = new double[] { 0.5, 0.6 };
. . .
trainX[9] = new double[] { 0.4, 0.7 }; // 1
trainX[10] = new double[] { 0.5, 0.7 };
. . .
trainX[18] = new double[] { 0.2, 0.6 }; // 2
. . .
trainX[27] = new double[] { 0.6, 0.3 };
int[][] trainY = new int[28][];
trainY[0] = new int[] { 1, 0, 0 }; // 0
trainY[1] = new int[] { 1, 0, 0 };
. . .
trainY[9] = new int[] { 0, 1, 0 }; // 1
trainY[10] = new int[] { 0, 1, 0 };
. . .
trainY[18] = new int[] { 0, 0, 1 }; // 2
. . .
trainY[27] = new int[] { 0, 0, 1 };
Console.WriteLine("Creating 2-15-3 RBF ");
RadialNet rn = new RadialNet(2, 15, 3, 0);
double lr = 0.005;
int maxEpoch = 1000;
double sigma = 0.1;
Console.WriteLine("Setting lr = " +
lr.ToString("F4") +
" maxEpoch = " + maxEpoch +
" sigma = " + sigma.ToString("F2"));
Console.WriteLine("Starting training");
rn.Train(trainX, trainY, lr, sigma, maxEpoch);
Console.WriteLine("Training complete");
double[] unk = new double[] { 0.15, 0.25 };
Console.WriteLine("Predicting class for: ");
ShowVector(unk, 2);
double[] p = rn.ComputeOutputs(unk);
Console.WriteLine("Predicted probs: ");
ShowVector(p, 4);
Console.WriteLine("End demo ");
Console.ReadLine();
} // Main
public static void ShowVector(double[] v,
int dec) { . . }
public static void ShowMatrix(double[][] m,
int dec) { . . }
} // Program class
class RadialNet
{
. . .
}
} // ns
All of the program control logic is contained in the Main() method. Helper functions ShowVector() and ShowMatrix() display a numeric vector or array-of-arrays style matrix using a specified number of digits after the decimal point.
The RBF network definition is contained in a class named RadialNet. All normal error checking has been removed to keep the main ideas as clear as possible.
The demo begins by setting up 28 hard-coded training items:
double[][] trainX = new double[28][];
trainX[0] = new double[] { 0.4, 0.6 };
trainX[1] = new double[] { 0.5, 0.6 };
. . .
int[][] trainY = new int[28][];
trainY[0] = new int[] { 1, 0, 0 };
trainY[1] = new int[] { 1, 0, 0 };
. . .
In a non-demo scenario, you'd likely store training data in a text file like:
0.4, 0.6, 1, 0, 0
0.5, 0.6, 1, 0, 0
. . .
0.6, 0.3, 0, 0, 1